O modelo regional se propõe a prever com maiores detalhes fenômenos associados a frentes, orografia, brisa marítima, tempestades severas, etc., enfim, sistemas organizados em mesoscala. Devido a maior não-linearidade dos sistemas nesta escala, a previsibilidade é menor e as previsões são de curto prazo. No caso do Eta, as previsões se estendem até 48h e cobrem a maior parte da América do Sul. Estas previsões são fornecidas duas vezes ao dia em uma grade regular com resolução de 40km.

Algumas das características principais do modelo Eta são brevemente descritas, e finalmente, um exemplo de previsão do modelo é apresentado.

1. Estrutura

a. Grade horizontal

A versão operacional do modelo possui resolução horizontal de 40km e existe também disponível uma versão com resolução de 80km. As equações do modelo são discretizadas para a grade E de Arakawa. A distância entre dois pontos adjacentes de massa ou de vento define a resolução da grade. A figura 1 mostra a distribuição dos pontos na grade E. Esta grade é regular em coordenadas esféricas, tendo o ponto de interseção entre o equador e o meridiano de 0o transladado para o centro do domínio. Desta forma a convergência entre os paralelos e meridianos são minimizados na região central do domínio. O domínio do modelo cobre aproximadamente a região compreendida entre as longitudes de 25oW a 90oW e as latitudes de 12oN a 45oS.

b. Coordenada vertical

Uma das características principais deste modelo é a coordenada vertical definida por Mesinger (1984):

onde:

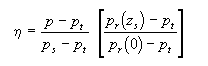
Esta coordenada se reduz à coordenada fazendo-se o termo entre colchetes igual a 1. A vantagem da coordenada é que as superfícies desta coordenada são aproximadamente horizontais, o que reduz os erros nos cálculos de variáveis obtidas a partir de derivadas horizontais. Estes erros são significativos em regiões de montanhas íngremes como é o caso dos Andes na América do Sul. O topo do modelo se encontra em 50mb.

As versões de 40km e 80km possuem 38 camadas , sendo a resolução maior nos baixos níveis e diminuindo com a altura; a primeira camada tem 20m de espessura. Um máximo secundário ocorre próximo à tropopausa para melhor descrever as frentes em altos níveis.

c. Orografia

A orografia do modelo ( Fig.2 ) é representada em forma de degraus cujo topo coincide com a interface das camadas . A altura de cada degrau é obtida a partir do método de silhueta. Este método procura o valor médio das alturas máximas da topografia dentro de cada quadrado de grade. Cada degrau possui um ponto de massa no centro e quatro pontos de velocidade localizados nos vértices.

2. Integração

a. Condições iniciais e de contorno

A condição inicial do modelo é obtida a partir de uma análise estática, onde a estimativa inicial é ajustada de acordo com as observacões do horário da análise. A previsão de 12h do modelo global do CPTEC é utilizada como estimativa inicial. Os erros entre as observações e as estimativas iniciais são minimizados através do método de interpolação ótima (OI). A análise é portanto realizada sobre uma grade de resolução correspondente à resolução do modelo global, e posteriormente, é interpolada para a grade do modelo Eta. As condições iniciais também podem ser obtidas a partir da análise do modelo global. A temperatura da superfície do mar é obtida do valor médio da semana anterior e é mantida constante durante a integração. O albedo inicial é obtido de uma climatologia sazonal.

Nos contornos laterais, o modelo é atualizado a cada 6 horas com as previsões do modelo global. As tendências nas bordas são distribuídas linearmente durante este período de 6h. Os contornos laterais possuem duas fileiras de pontos que são excluídas da integração do modelo.

b. Dinâmica

As variáveis prognósticas do modelo são: temperatura do ar, componentes zonal e meridional do vento, umidade específica, pressão à superfície e energia cinética turbulenta. A integração no tempo utiliza a técnica de 'split-explicit' (Gadd, 1978) onde os termos devido ao ajuste pelas ondas de gravidade inerciais são integrados separadamente dos termos devido à advecção. Um esquema 'forward-backward' modificado por Janjic (1979) trata dos termos responsáveis pelo ajuste, enquanto o esquema 'Euler-backward' modificado trata dos termos de advecção horizontal e vertical. O passo de tempo fundamental do modelo é o do ajuste, que equivale à metade do passo de tempo da advecção.

O esquema de diferenças finitas no espaço emprega o método de Janjic (1984) que controla o falso escoamento de energia para as ondas mais curtas. Um amortecimento na divergência combinado com uma difusão horizontal não-linear de 2a ordem mantém os campos suaves.

c. Física

O modelo utiliza um esquema de Betts-Miller modificado para parametrizar a convecção (Janjic, 1994). A condensação de larga escala ocorre quando a umidade relativa excede 95%. Os processos turbulentos na atmosfera livre são tratados através do esquema de Mellor-Yamada nível 2.5 que calcula a energia cinética turbulenta e os fluxos verticais. O esquema Mellor-Yamada 2.0 é utilizado na primeira camada do modelo (Mellor e Yamada, 1974) para representar a turbulência na camada superficial. O esquema de parametrização de radiação de ondas longas (Fels e Schwarzkopf, 1975) e curtas (Lacis e Hansen, 1974) foi desenvolvido pelo Geophysical Fluid Dynamics Laboratory.

3. Exemplo de previsão

A figura 3 mostra uma previsão de precipitação acumulada em 24h válida para 12UTC de 10 de junho de 1995. A resolução de 40km foi utilizada. Esta foi uma previsão de 36h que teve como condição inicial a análise do modelo global do NCEP na resolução T126L28. Os núcleos de máxima precipitação, que não foram previstos pelo mesmo modelo global, apresentaram valores um pouco abaixo daqueles observados ( figura 4 ). Este foi um caso de intensa precipitação sobre a região Sul que ocorreu devido à passagem de um cavado de onda curta (Climanálise, 1995). Neste exemplo, o aumento da resolução horizontal permitiu que um sistema subsinótico fosse melhor reproduzido, beneficiando assim a qualidade da previsão.

Referências Bibliográficas:

Black, T. L., 1994: The new NMC mesoscale Eta model: Description and forecast examples. Wea. and Forecasting, 9, 265-278.

Climanálise 1995- Boletim de Monitoramento e Análise Climática. Cachoeira Paulista, SP, Brasil, INPE/CPTEC. vol.10, No 6.

Fels, S. B., e M. D. Schwarzkopf, 1975: The simplified exchange approximation: A new method for radiative transfer calculations. J. Atmos. Sci., 32, 1475-1488.

Gadd, A. J., 1978: A split-explicit integration scheme for numerical weather prediction. Quart. J. Roy. Met. Soc., 104, 569-582.

Janjic, Z.I., 1979: Forward-backward scheme modified to prevent two-grid-internal noise and its application in sigma coordinate models. Contrib. Atmos. Phys., 52, 69-84.

Janjic, Z.I., 1984: Nonlinear advection schemes and energy cascade on semi-staggered grids. Mon. Wea. Rev., 112, 1234- 1245.

Janjic, Z.I., 1994:The step-mountain Eta coordinate Model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. J. Atmos. Sci., 122, 927-945.

Lacis, A. A., e J. E. Hansen, 1974: A parameterization of the absortion of solar radiation in the earth's atmosphere. J. Atmos. Sci., 31, 118-133.

Mellor, G. L., Yamada, T., 1974: A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci., 31, 1791-1806.

Mesinger, F., 1984: A blocking technique for representation of mountains in atmospheric models. Riv. Meteor. Aeronautica, 44, 195--202.

Mesinger, F., Z. I. Janjic, S. Nickovic, D. Gavrilov, e D. G. Deaven, 1988: The step-mountain coordinate: Model description and performance for cases of Alpine lee cyclogenesis and for a case of Appalachian redevelopment. Mon. Wea. Rev., 116, 1493-1518.