O Regional Atmospheric Modeling System (RAMS) foi desenvolvido na Colorado State University para unificar vários códigos existentes de simulação numérica de tempo (Pielke,1974; Tripoli e Cotton, 1982; Tremback et al., 1985). Concluiu-se que a unificação desses códigos, mantendo-se os atributos originais de cada um , facilitava mais efetivamente a pesquisa científica no Departamento de Ciências Atmosféricas da Universidade Estadual do Colorado. Além disso, na fusão dos modelos uma gama de melhorias foram introduzidas no RAMS, entre as quais a capacidade de aninhamento de grades, que é uma das mais importantes. Baseado no método de grades iterativas de Clark e Farley (1984), o RAMS possui a habilidade para representar a larga escala, e então aninhar-se progressivamente para escalas menores. Mais do que uma grade aninhada pode ser setada dentro do grid de grande escala. As figuras 1, 2, 3 e 4 exemplificam um aninhamento de grades, onde na figura 1 temos o campo de larga escala fornecido como condições de contorno para o modelo RAMS, a figura 2 mostra a previsão obtida pelo RAMS com uma resolução de 80km, a figura 3 mostra o mesmo campo válido para o mesmo horário aninhado à primeira grade com uma resolução de 40Km, e a figura 4 mostra o mesmo campo válido para o mesmo horário aninhado à segunda grade com uma resolução de 20Km. Notamos que com essa capacidade podemos obter, com o RAMS, um melhor detalhamento dos campos. Na figura 5 temos uma visão de como é feito o aninhamento. O RAMS possui uma opção não hidrostática para que todas as escalas espaciais meteorológicas relevantes possam ser representadas. O conceito de módulos "plug-compatible" (Pielke e Aritt, 1984) é usado no RAMS para fazer a assistência no desenvolvimento de parametrizações de interfaces no RAMS. O termo Plug-compatible quer dizer que a interface entre as subrotinas (i.é., os módulos) e o resto do RAMS é claramente definido pelos usuários do código. Características atuais e opções do RAMS são mostradas na Tabela 1 (Pielke et al., 1992) . Um detalhado overview do RAMS e suas opções é dado em Walko e Tremback (1991).

Inicialização e Análise

Análise Sinótica

O RAMS inclui o Isentropic ANalise package (RAMS/ISAN) como opção 4 de inicialização (ver Tabela 1.) que realiza a tarefa de análise de dados para as condições iniciais e de fronteiras para rodadas de grande escala. Considerando que o fluxo de escala sinótica é, em uma primeira aproximação, adiabático, uma análise objetiva feita numa superfície isentrópica irá melhorar a aproximação da variabilidade inter estações dos campos atmosféricos. As isentrópicas tendem a se compactar nas áreas frontais, aumentando assim a resolução ao longo das descontinuidades. Finalmente, porque as isentrópicas são inclinadas nas proximidades das frentes, características de comprimentos de onda curta em coordenadas cartesianas são transformadas em sistemas isentrópicos com características de comprimentos de onda longa, que podem ser objetivamente analisadas com muito menos suavização que com outros sistemas de coordenadas. Há algumas desvantagens nas coordenadas isentrópicas, que são, a resolução vertical decresce com o decréscimo da estabilidade atmosférica. (i.é., na camada limite planetária), e as isentrópicas freqüentemente interceptam a terra.

RAMS/ISAN tem a habilidade de combinar ou misturar alguns conjuntos de dados para análise e uma estrutura modular simplifica a inserção de dados não convencionais. O código corrente suporta análises globais do NMC e ECMWF, radiosonda do NMC e dados observacionais de superfície, todos no formato do NCAR. Todos os níveis mandatários de vento, temperatura e umidade podem ser usados a partir de observações de radiosondas. Podemos também assimilar dados de sondagens especiais, falsas sondagens, ou alguma observação adicional de superfície que são disponíveis. O código é também incivilizado com NOAA Forecast System Laboratory MAPS (Mesoscale Analysis and Prediction System). A técnica de análise de dados pode ser sumarizada como se segue. As componentes horizontais do vento, pressão e umidade relativa a partir da grade da análise global e alguns dados de radiosonda disponíveis são interpolados verticalmente (linearmente em pR/Cp) para níveis isentrópicos. O esquema de análise objetiva de Barnes (1973) é então aplicado para essas variáveis nas superfícies isentrópicas com o uso de parâmetros específicos no esquema de controle da intensidade de suavização. Depois que as variáveis foram objetivamente analisadas, a função de corrente Montgomery é então obtida em uma integração hidrostática a partir da análise objetiva das funções de corrente "condições de contorno" num nível isentrópico próximo da tropopausa. Algumas interpolações horizontais são usadas sobrepondo a técnica polinomial de Bleck e Haagenson (1968).

As variáveis atmosféricas na superfície terrestre são analisadas de uma maneira similar às variáveis de níveis superiores. Componentes de vento, temperatura potencial e umidade relativa são objetivamente analisadas. Pressão e função de corrente Montgomery são obtidas hidrostaticamente a partir do primeiro nível isentrópico abaixo da terra.

Como a análise isentrópica é completa, as variáveis atmosféricas e topografia são transferidas para o modelo usando superposição de interpolações polinomiais. Primeiro, as componentes do vento, função de corrente Montgomery, e umidade relativa são interpoladas de uma superfície isentrópica para a grade do modelo. A altura da superfície isentrópica pode ser estabelecida e o vento, temperatura potencial e umidade relativa são interpoladas linearmente na altura para os níveis na coordenada z. Uma última integração hidrostática é feita para encontrar a pressão na grade do modelo.

Nudging

Assimilação de dados em 4 dimensões (4DDA) implica uma integração eficaz dos dados observacionais dependentes do tempo num modelo prognóstico. Isto pode ser feito nos estágios iniciais de uma rodada do modelo como uma relaxação Newtoniana (mais comumente conhecida como "nudging") ou num esquema variacional como método adjacente.

No esquema de nudging um termo de tendência extra é adicionado para cada equação prognóstica, que força a variável prevista em direção às observações.

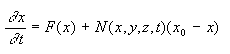
Onde x é a variável do modelo , F(x) representa a física do modelo, N(x,y,z,t) é o peso do nudging, e x0 a observação da variável do modelo (Wang e Warner, 1988).

Referências Bibliográficas

Atwater, M. A., Brown Jr., P. S., 1974: Numerical calculation of the latitudinal variation of solar radiation for an atmosphere of varying opacity. J. Appl. Meteor. 13, 289-297.

Avissar, R., Mahrer, Y., 1988: Mapping frost-sensitive areas with a tree-dimensional local-scale numerical model. Part I: Physical and numerical aspects. J. Appl. Meteor. 27, 400-413.

Barnes, S. L., 1973: Mesoscale objetive map analysis using weighted time-series observations. NOAA Tech. Memo. ERL NSSL-62 [NTIS COM-73-10781], March. National Severe Storms Laboratory. Norman, Oklahoma, 60pp.

Bleck, R., Haagenson, P. L., 1968: Objective analysis on isentropic surfaces, NCAR Tech. Note, TN-39, December, National Center for Atmospheric Research, Boulder, Colorado. 27pp.

Chen, C., Cotton, W. R., 1983: A one-dimensional simulation of the stratocumulus-capped mixed layer. Bound-Layer Meteor. 25, 289-321.

Chen. C, Cotton, W. R., 1987. The physics of the marine stratos cumulus-capped mixed layer. J. Atmos. Sci.. 44, 2951-2977.

Clark, T. L., Farley, R. D., 1984: Svere downslope windstorm calculations in two and three spatial dimentions using anelastic interative grid nesting. A possible mechanism for gustmess. J. Atmos. Sci.. 41, 329-350.

Cotton, W. R., Stephens, M. A., Nehrkorn, T., Tripoli, G. J., 1982: The Colorado State University three-dimensional cloud/mesoscale model - 1982. Part II: An ice phase parameterization. J. de Rech. Atmos.. 16, 295-320.

Cotton, W. R., Tripoli, G. J., Rauber, R. M., Mulvihill, E. A., 1986: Numerical simulation of the effects of varying ice crystal nucleation rates and aggregation processes on orographic snowfall. J. Climate Appl. Meteor.. 25, 1658-1680.

Cram, J. M., 1990: Numerical simulation and analysis of the propagation of a prefrontal squall line. Ph.D. dissertation, Dept. of Atmospheric Science, Colorado State University, Ft. Collins, CO, 330pp.

Davies, H. C., 1983: Limitations of some common lateralboundary schemes used in regional NWP models. Mon. Wea. Rev.. 111, 1002-1012.

Deadorff, J. W., 1980: Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound. Layer Meteor.. 18, 495-527.

Herman, G., Goody, R., 1976: Formation and persistence of summertime arctic stratus clouds. J. Atmos. Sci.. 33, 1537-1553.

Jacobs, C. A., Pandolfo, J. P., Atwater, M. A., 1974: A description of a general three dimensional numerical simulation model of a coupled air-water and/or air-land boundary layer. IFYGL final report, CEM Report No. 5131-509a. The Center for the Environment and Man. Hartford, Conecticut.

Klemp, J. B., Durran, D. R., 1983: An upper boundary condition permitting internal gravity wave radiation in numerical mesoscale models. Mon. Wea. Rev. 111, 430-444.

Klemp, J. B., Lilly, D. K., 1978: Numerical simulation of hydrostatic mountain waves. J. Atmos. Sci.. 35, 78-107.

Klemp, J. B., Wilhelmson, R. B., 1978a: The simulation of three-dimensional convective storm dynamics. J. Atmos. Sci.. 35, 1070-1096.

Klemp, J. B., Wilhelmson, R. B., 1978b:Simulations of right and left-moving storms produced through storms splitting. J. Atmos. Sci.. 35, 1097-1110.

Kondrat'yev, J., 1969: Radiation in Atmosphere. New York: Academic Press. 912pp.

Lacis, A. A., Hansen, J., 1974: A parameterization for the absortion of solar radiation in earth's atmosphere. J. Atmos. Sci.. 31, 118-133.

Lee, T. J., Pielke, R. A., 1992: Estimating the soil surface specific humidity. J. Appl. Meteor.. 31, 480-484.

Louis, J. F., 1979: A parametric model of vertical eddy fluxes in the atmosphere. Bound-Layer Meteor.. 17, 187-202.

Mahrer, Y., Pielke, R. A., 1977: A numerical study of the airflow over irregular terrain. Beitrage zur Physik der Atmosphare. 50, 98-113.

McCumber, M. C., Pielke, R. A., 1981: Simulation of the effects of surface fluxes of heat and moisture in a mesoscale numerical model. Part I: Soil layer. J. Geophys. Res.. 86, 9929-9938.

McDonald, J. E., 1960: Direct absorption of solar radiation by atmospheric water vapor. J. Meteor.. 17, 319-328.

McNider, R. T., 1981: Investigation of the impactof topographic circulation on the transport and dispersion of air pollutants. Ph.D. Dissertation, University of Virginia. Charlottesville, Virginia. 210pp.

McNider, R. T., Pielke, R. A. 1981: Diurnal boundary-layer development over sloping terrain. J. Atmos. Sci.. 38, 2198-2212.

McNider, R. T., Moran, M. D., Pielke, R. A., 1988: Influence of diurnal and inertial boundary layer oscilations on long-range dispersion. Atmos. Environ.. 22, 2445-2462.

Meyers, M. P., DeMott, P. J., Cotton, W. R., 1992: New primary ice nucleation parameterizations in an explicit cloud model. J. Appl. Meteor.. 31, 708-721.

Orlanski, I., 1976: A simple boundary condition for undounded hyperbolic flows. J. Comput. Phys.. 21, 251-269.

Perkey, D. J., Kreitzberg, C. W., 1976: A time-dependent lateral boundary scheme for limited-area primitive equation models. Mon. Wea. Rev.. 104, 744-755.

Pielke, R. A., 1974: Mesoscale Meterological Modeling. New York, N.Y.: Academic Press, 612pp.

Pielke, R. E., Arritt, R. W., 1984: A proposal to standardizemodels. Bull. Amer. Meteor. Soc.. 65, 1082.

Pielke, R. E., Cotton, W. R., Walko, R. L., Tremback, C. J., Lyons, W. A., Grasso, L. D., Nicholls, M. E., Moran, M. D., Wesley, D. A., Lee, T. J., and Copeland, J. H., 1992: A Comprehensive Meteorological Modeling System - RAMS. Metero. Atmos. Phys.. 49, 69-91.

Rodgers, C. D., 1967:The use of emissivity in atmospheric radiation calculations. Quart. J. Roy. Meteor. Soc.. 93, 43-54.

Sassamori, T., 1972: A linear harmonic analysis of atmospheric motion with radiative dissipation. J. Meteor. Soc. Japan. 50, 505-518.

Stephens, G. L., 1977: The transfer of radiation in cloudy atmosphere. Ph.D. dssertation. Meteorology Departament, University of Melbourne, Australia. 396pp.

Stephens, G. L., 1978: Radiation profiles in extended water clouds. Theory. J. Atmos. Sci.. 35, 2111-2122.

Tremback, C. J., 1990: Numerical simulation of a mesoscale convective complex model development and numerical results. Ph.D. dissertation, Atmos. Sci. Paper No. 465, Department of Atmospheric Science, Colorado State University, FortCollins, CO 80523, 247pp.

Tremback, C. J., Kessler, R., 1985: A surface temperature and moisture parameterization for use in mesoscale numerical models. Preprints. 7th AMS Conference on Numerical Weather Prediction. June 17-20. Montreal, Quebec, Canada, Amer. Meteor. Soc., Boston. 355-358.

Tremback, C. J., Tripoli, G. J., Cotton, W. R., 1985: A regional scale atmospheric numerical model including eplicit moist physics and a hydrostatic time-split scheme. Preprints, 7th AMS Conference on numerical Weather Prediction, June 17-20. Montreal, Quebec, Canada, Amer. Meteor. Soc., Boston. 433-434.

Tremback, C. J., Powell, J., Cotton, W. R., Pielke, R. A., 1987: The forward-in-time upstream advection scheme: Extension to higher orders. Mon. Wea. Rev.. 115, 540-555.

Tripoli, G. J., Cotton, W. R., 1980: A numerical investigation of several factors contributing to the observed variable intensity of deep convection over south Florida. J. App. Meteor.. 19, 1037-1063.

Tripoli, G. J., Cotton, W. R., 1982: The Colorado State University three-dimensional cloud mesoscale model, 1982: PartI: General theoretical framework and sensitivity experiments. J. de Rech. Atmos.. 16, 185-220.

Tripoli, G. J., Coton, W. R., 1986: An intense quasi-steady thunderstorm over mountamous terrain. Part IV: Three-dimensional numerical simulation. J. Atmos. Sci.. 43, 896-914.

Uliasz, M., 1993: Atmospheric mesoscale dispersin modeling system - MDMS. J. Appl. Meteor. (in press).

Walko, R. L., Tremback, C. J., 1991: RAMS - The Regional Atmospheric odeling System Version 2C: User's guide. Published by ASTeR, Inc., P.O. Box 466, Fort ollins, Colorado. 86pp.

Wang, W., Warner, T. T., 1988: Use of four-dimensional data assimilation by Newtonian relaxation and latent-heat forcing to improve a mesoscale-model precipitation forecast: A case study. Mon. Wea. Rev.. 116, 2593-2613.

Yamamoto, C., 1962: Direct absortion of solar radiation by atmospheric water vapor, carbon dioxide and molecular oxygen. J. Atmos. Sci.. 19, 182-188.

Tabela 1. Características e Opções do modelo. Tabela 1.

Tabela 1. Continuação a Tabela 1.

Tabela 1. Continuação b Tabela 1.