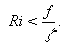 Longe das correntes de jato,
Longe das correntes de jato,
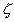 =f, o que reduz o critério de ISS para Ri < 1 .
=f, o que reduz o critério de ISS para Ri < 1 .
atmosfera saturada a instabilidade segue o critério de ISC. O
critério para uma atmosfera saturada ou próxima da
saturação é menos restritivo do que no caso seco ou de
ISS.
A presença de instabilidade simétrica foi detectada durante a
integração do modelo global do ECMWF[1
em T106L31 (Chou, 1994). A freqüência de ocorrência foi
comparável à da convecção de nível
médio. A forma úmida da instabilidade ocorre preferencialmente
nas latitudes médias, enquanto que a forma seca, nas baixas latitudes.
]
3. A Aplicação Dos Critérios de Instabilidade
SImétrica Condicional a uma Situação Observada
Parsons e Hobbs (1983) sugerem que as bandas amplas de
precipitação no setor quente (entre a frente fria e a quente)
paralelas à frente fria e as bandas amplas frontais frias estejam
associadas à ISC.
Um caso de ISC foi observado em 21 de julho de 1996, utilizando-se dados das
análises do NCEP [2 das 12 UTC. Uma
seção vertical meridional de superfícies] Mg e
ea, com regiões de movimento ascendente, qe < 0 e
condicionalmente estáveis ou neutras, é mostrada na Fig. 2 a e
b. A seção foi construída perpendicularmente às
linhas de espessura da camada 850/300 hPa, com o eixo horizontal apontando
para o lado mais quente ou de maiores valores de espessura (Fig. 3).
A seção vertical (Fig. 2 a,b) está localizada ao longo de
41.25 W. Na Fig. 2a observa-se movimento ascendente acima de 600 hPa dentro de
uma região onde o critério de ISC é satisfeito, como
indicado na Fig. 2 b pela região amarela com valores de qe
< 0 .
A configuração dos núcleos de movimento ascendente exibem
uma ligeira inclinação e localizam-se aproximadamente sobre a
área de nebulosidade com estrutura de banda ao norte do Estado Rio de
Janeiro, já no setor quente ou pré-frontal, de acordo com a foto
do satélite MET-5 (Fig. 4 a), no canal infravermelho. Na Fig. 4 b,
observa-se o campo estimado de precipitação a partir das imagens
do satélite GOES-8 (canal infravermelho) de 21 de julho de 1996 de 09 e
15 UTC (precipitação resultante da soma das estimativas das
imagens de 09 e 15 UTC). Para estimativa foi empregada a "Convective Stratiform
Technique" (CST). Em especial, a CST consegue separar a
precipitação convectiva da estratiforme (Härter e Scofield,
1996). A precipitação estimada entre 23 e 22deg.S (região
onde o critério de ISC é satisfeito entre 625 e 325 hPa)
está em torno de 20 mm e apresenta uma estrutura paralela às
linhas de espessura (Fig. 3).
A região de movimento ascendente em baixos níveis assemelha-se
à ascensão presente na rampa frontal e está relacionada
à instabilidade condicional convectiva. Igualmente, observa-se, no
setor frio da região frontal, a presença de instabilidade
convectiva misturada às áreas neutras e de ISC, com o
núcleo de movimento ascendente bastante inclinado, ao contrário
do movimento ascendente presente nos níveis superiores (setor quente),
onde há fraca ou nenhuma instabilidade condicional convectiva associada.
O presente caso tem por objetivo ilustrar uma situação onde
é observado movimento ascendente relativamente forte, em regiões
da atmosfera com fraca ou mesmo sem instabilidade convectiva e, provavelmente,
associado à ISC.
Nunes e Innocentini (1990) estudaram casos de precipitação em
forma de banda sobre o Estado de São Paulo, e procuraram estabelecer uma
possível relação entre o aparecimento das bandas de
precipitação e a presença de IS. Alguns casos de banda
forte (duração da estrutura de banda > 3 h), banda fraca (
< 3h) e situações sem banda ou até mesmo sem
precipitação foram comparadas para deslocamentos ascendentes da
parcela de dois tipos: puramente vertical e inclinado. Os perfis de
temperatura potencial virtual, no caso do deslocamento ascendente inclinado,
indicaram maior quantidade de energia disponível apenas nos casos de
banda, o que não foi tão bem representado para os deslocamentos
ascendentes verticais.
Agradecimentos: - A autora agradece à Dra. Chou Sin Chan e ao
Dr. Valdir Innocentini por seus valiosos comentários.
Referências Bibliográficas
Bennetts, D.A.; Hoskins, B.J. Conditional symmetric instability - a
possible explanation for frontal rainbands. Quarterly Journal of the Royal
Meteorological Society, 105(446):945-962, Oct. 1979.
Bennetts, D.A.; Sharp, J.C. The relevance of conditional symmetric
instability to the prediction of mesoscale frontal rainbands. Quarterly
Journal of the Royal Meteorological Society, 108,(457):595-602,
July 1982.
Bjerknes, J. On the structure of moving cyclones. Geofys. Publikasjoner
Norske Videnskaps-Akad., 1(2):1-8, 1919. Apud Emanuel
(1983).
Chou, S.C. Presença de instabilidade simétrica em um modelo de
grande escala. VII Congresso Brasileiro de Meteorologia, Belo
Horizonte, MG, 1994.
Emanuel, K.A. Inertial instability and mesoscale convective systems. Part
I: Linear theory instability in rotating viscous fluid. Journal of the
Atmospheric Sciences, 36(12):2425-2449, Dec. 1979.
______ On assessing local condicional symmetric instability from atmospheric
soundings. Monthly Weather Review, 111(10):2016-2033, Oct.
1983.
______ Frontal circulations in the presence of small moist symmetric
stability. Journal of the Atmospheric Sciences,
42(10):1062-1071, May 1985.
Härter, F.P.; Scofield, G.B. Descrição das técnicas
GPI, NWAT e CST. Curso de Estimativa de Precipitação por
Satélite, CPTEC, Cachoeira Paulista, 1996. pp.8
Innocentini, V.; Caetano Neto, E.S. A numerical study of the role of
humidity in the updraft driven by moist slantwise convection. Journal of
the Atmospheric Sciences, 49(13):1092-1106, July 1992.
Nunes, A.M.B.; Innocentini, V. O papel da instabilidade simétrica
condicional no dessenvolvimento das bandas de precipitação.
VI Congresso Brasileiro de Meteorologia, Salvador, BA, 1990.
Parsons, D.B.; Hobbs, P.V. The mesoscale and microscale structure and
organization of clouds and precipitation in midlatitude cyclones. XI:
Comparisons between observational and theoretical aspects of rainbands.
Journal of the Atmospheric Sciences, 40(10):2377-2397, Oct.
1983.
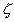 < 0 (estável), =
< 0 (estável), =
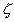 =0 (neutro) e
=0 (neutro) e 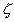 > 0 (instável), onde
> 0 (instável), onde 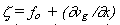 (vg x) é a componente vertical da vorticidade absoluta,
fo representa o valor médio do parâmetro de Coriolis num
dado intervalo espacial; e vg é o vento geostrófico
perpendicular ao eixo x, sendo x a direção perpendicular
à banda de precipitação.
(vg x) é a componente vertical da vorticidade absoluta,
fo representa o valor médio do parâmetro de Coriolis num
dado intervalo espacial; e vg é o vento geostrófico
perpendicular ao eixo x, sendo x a direção perpendicular
à banda de precipitação. 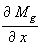 > 0 inercialmente instável,
> 0 inercialmente instável,
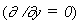 ), onde os processos dissipativos e
turbulentos são desprezados:
), onde os processos dissipativos e
turbulentos são desprezados:
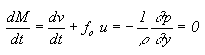
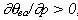 < 0. No caso estável, -
< 0. No caso estável, -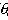 ea representa a temperatura potencial
equivalente do ambiente. A aceleração vertical de uma parcela
que conserva a temperatura potencial equivalente,
ea representa a temperatura potencial
equivalente do ambiente. A aceleração vertical de uma parcela
que conserva a temperatura potencial equivalente, 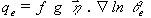 , e pode ser definido como a vorticidade potencial de Ertel para o ar saturado
multiplicada pelo parâmetro de Coriolis, sendo que
, e pode ser definido como a vorticidade potencial de Ertel para o ar saturado
multiplicada pelo parâmetro de Coriolis, sendo que 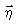 é o vetor vorticidade absoluta. No plano x-z, as
componentes de
é o vetor vorticidade absoluta. No plano x-z, as
componentes de 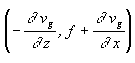 ,
,
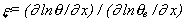 , onde o parâmetro
, onde o parâmetro 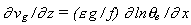 é aproximadamente 0,5 perto da superfície e 1
nas proximidades da tropopausa. A equação anterior se reduz
à:
é aproximadamente 0,5 perto da superfície e 1
nas proximidades da tropopausa. A equação anterior se reduz
à: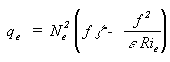
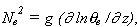 = g ( lne / z), onde Ne é a
freqüência de Brunt-Väisällä para o ar saturado; e
= g ( lne / z), onde Ne é a
freqüência de Brunt-Väisällä para o ar saturado; e
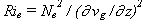 representa o
número de Richardson equivalente.
representa o
número de Richardson equivalente. 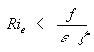 A expressão anterior é análoga àquela referente a
inclinação das superfícies Mg em
relação às
A expressão anterior é análoga àquela referente a
inclinação das superfícies Mg em
relação às 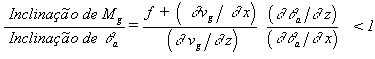
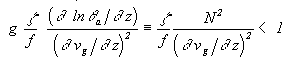
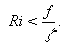 Longe das correntes de jato,
Longe das correntes de jato,